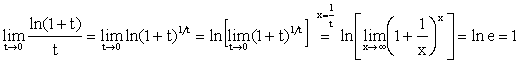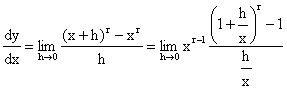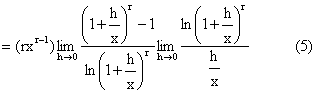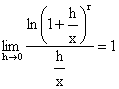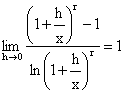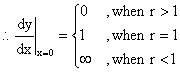Differentiate x^r

Doubt

We use the derivative formula:

very often. However, can the formula be extended to the case where n is a real number?

In proving (1), most textbooks use Binomial Theorem, which depends on the Principle of Mathematical Induction. Since Mathematical Induction deals with natural numbers, (1) is good for natural numbers only.

Therefore it is not good to use (1) to write:

We therefore like to prove:

Starting Point

We suppose the reader know how to get the important constant e:

Equation (3) involves the study of Monotone convergence theorem of sequences and the extension of sequences to functions by Sandwich theorem. You can find the details in most textbooks.

From (3), we can get:

Proof of (4):

The main proof

Let y = x^r, r Î R, r ¹ 0

(1) When x ¹ 0,

It seems that (5) is difficult. But you can observe that:

(a) rx^r-1 is independent of h. It is moved out of the limit and is of desired result.

(b) We break into two limits because we can get by (4) the result:

(c) We can also use (4) to show that:

by putting in (4),

\ The derivative formula (2) is proved.

(2) When x = 0,