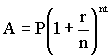Continuous Compound Interest
Problem If you have an amount $P, and you place it in a bank with annual interest rate, r%, for t years, what is your amount if the compound interest is calculated yearly, monthly, daily, hourly, or even in every minute, second and continuously….
From finite to infinite With the notations in the above, if we can get $A (interest and principal) in which $P is compounded n times per year, you will get after t years the amount: If we allow n to increase indefinitely, then we have the case of continuous compound interest.
Constant e
Example If you have an amount $1000 and invest in a bank at annual interest rate 6% and compounded monthly, then after 10 years, you will get back: However, if the amount is compounded continuously, you will get back after 10 years: A(¥) = $1000 e^0.06^´^10 » $1822.12
Doubling your money To double your money, you have A(¥) = 2A Ae^rt = 2A e^rt = 2 rt = ln 2 t = ln 2 / r » 0.693 / r (*) As in the example above, the amount you get from continuous compound interest and monthly compound interest do not differ very much within reasonable range of interest rate. So if the interest rate is 0.06, you expect your money double in : t = ln 2 / 0.06 » 11.55 or roughly 12 years.