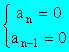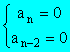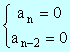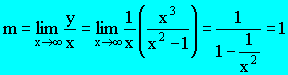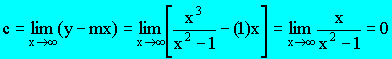Algebraic method in finding the asymptote of a curve

What is an asymptote of a curve?

An asymptote of the curve y = f(x) (or in implicit form: f(x,y) = 0) is a straight line such that the distance between the curve and the straight line lends to zero when the points on the curve approach infinity. There are three types of asymptotes, namely, vertical, horizontal and oblique asymptotes. Here is an algebraic method for finding oblique (and also horizontal) asymptotes of algebraic curves.

The method

(1) Replace y by mx + c in the equation of the curve and arrange the result in the form :

(2) Solve the simultaneous equation :

(3) For each pair of solutions of m and c, write the equation of an asymptote y = mx + c.

(4) If there is no term in (1), solve :

instead of the set of simultaneous equation in (2).

Reason for (2) above

The equation

has a double root at infinity.

Put ,

The equation becomes

Then the equation has a double root at y = 0.

That is, the equation is of the form:

Therefore :

Example

Find the oblique asymptotes of

Solution

Put y = mx + c in

\ (x² - 1)(mx+c) = x³.

\ (m-1)x³ - cx² - mx -c = 0 (1)

Put y = 1/x in (1),

\ cy³ + my² + cy - (m-1) = 0 (2)

y = mx + c is an asymptote of

iff there is a double root at infinity for (1)

iff there is a double root at 0 for (2).

\ m - 1 = 0 and c = 0.

\ m = 1 and c = 0.

\ The oblique asymptote is y = x.

Appendix (Calculus method)

\ The oblique asymptote is y = x.