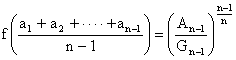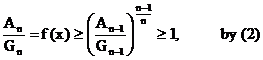Proof of A.M. ³ G.M. by differentiation

Finding Minimum by calculus first

Given a₁ > 0, a₂ > 0, …, a_n > 0, determine the minimum of

for x > 0.

Solution

Taking logarithm and finding derivative

Differentiate, we get:

…..(1)

Test for minumum

For critical value , f’(x) = 0

\

(i) When

From (1) and since f(x) > 0, f’(x) < 0

(ii) When

From (1) and since f(x) > 0, f’(x) > 0.

The minimum

\ f(x) attains its minimum when

Prove by mathematical induction

We then use the previous result to show that:

Solution

From previous result, for all x, we have

Let P(n) be the proposition : “A _n ³ G _n.”

For P(1), A₁ = a₁ = G₁. \ P(1) is true.

Assume P(n-1) is true for some integer n.

that is, A _n-1³ G _n-1.

For P(n), By (3), putting x = a_n.

\ P(n) is true.

\ By the Principle of Mathematical Induction, A _n ³ G _n is true " nÎN.

Final note

You can start by showing that the function:

attains its minimum at